How To Find The Area Of An Irregular Pentagon

So we have learned how to find the surface area of an irregular polygon with the assist of the shoelace formula (or the shoelace theorem):

Area = 0.v * |(x_aney₂ - y₁x₂) + (ten₂y_three - y₂x₃) + ... + (x_n-1y_n - y_n-1x_n) + (10_ny_one - y_nx_ane)|

But why, WHY is it chosen the shoelace formula? It'southward about polygons and calculations, not nearly shoes and laces, right? That's correct, merely we will bear witness you at present that at that place is a reason behind this term. And, thank you to such a foreign name, you hopefully have a better chance of remembering this formula!

So, let u.s. list the coordinates of the vertices of our polygon in a cavalcade as follows:

x₁, y₁

ten₂, y₂

x₃, y₃

...

xₙ₋₁, yₙ₋₁

xₙ, yₙ

x₁, y₁

As you lot can encounter, the start vertex appears once again at the end of the list.

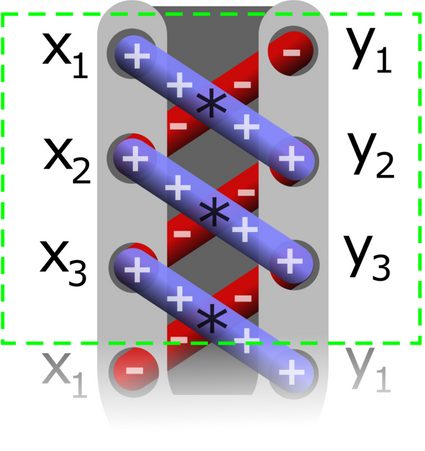
At present, to get the expression nether the modulus at the correct-hand side of the shoelace formula, nosotros go from the peak to the bottom of our column and mark the pairs of numbers to be multiplied. Doing then, we arrive at the paradigm that resembles laced-upwardly shoes - as in the moving picture below.

It is vital you recall that for each pair of rows:

When we multiply the upper-left and lesser-right numbers, we take their product with the + sign.
When we multiply the upper-right and bottom-left numbers, we have their production with the - sign.

Shoelace formula illustration — Job Bouwman, CC BY-SA iv.0, via Wikimedia Commons

For those of you familiar with matrices, there is ane more way to recollect the shoelace formula. Namely, we can express the expanse of our polygon as 0.v times the sum of the determinants of the following 2x2 matrices: