How To Find The Inverse Of A Matric

Matrix Inversion:
Finding the Changed of a Matrix (page one of two)

---

For matrices, there is no such affair every bit sectionalisation. You lot can add, decrease , and multiply matrices, but you cannot divide them. There is a related concept, though, which is called "inversion". Beginning I'll discuss why inversion is useful, then I'll bear witness you how to do information technology .

---

Think back to when y'all first learned about how to solve linear equations . If yous were given something like " three x = 6 ", you would solve by dividing both sides by 3 . Since multiplying by 1/iii i s the same equally dividing by iii , you could also multiply both sides by 1/3 to become the same respond: 10 = 2 . If you needed to solve something similar "(iii/ii)x = six" , you could still dissever both sides by 3/2, but it was probably easier to multiply both side by 2/three. The reciprocal fraction 2/three is the inverse of 3/two considering, if yous multiply the 2 fractions, y'all get 1 , which is, in this context, chosen "the (multiplicative) identity ": i is chosen the identity because multiplying something by one doesn't change its value.

This terminology and these facts are very important for matrices. If you are given a matrix equation similar AX = C , where you are given A and C and are told to figure out 10 , yous would like to "split up off" the matrix A . But you tin can't do sectionalization with matrices. On the other paw, what if you could observe the inverse of A , something similar to finding the reciprocal fraction in a higher place? The inverse of A , written every bit " A ^�one " and pronounced " A changed", would permit you to cancel off the A from the matrix equation and so solve for X .

AX = C
A ^�1 AX = A ^�1 C
IX = A ^�1 C
Ten = A ^�1 C

How did " A ^�1 AX " on the left-manus side of the equation turn into " X "? Recall back to the nature of inverses for regular numbers. If you have a number (such every bit three/2 ) and its inverse (in this case, 2/3 ) and you multiply them, y'all get 1 . And 1 is the identity, so called because i 10 = 10 for whatsoever number x . It works the same manner for matrices. If you multiply a matrix (such as A ) and its inverse (in this case,
A ^�ane ), y'all get the identity matrix I . And the signal of the identity matrix is that Ix = X for any matrix X (meaning "any matrix of the right size", of form).

It should be noted that the order in the multiplication above is important and is non at all arbitrary. Recall that, for matrices, multiplication is not commutative. That is, AB is almost never equal to BA . So multiplying the matrix equation "on the left" (to become A ^�1 AX ) is not at all the same affair equally multiplying "on the right" (to get AXA ^�i ). And you tin not say that the production AXA ^�one  equals A ^�ane AX , considering you can't switch around the gild in the multiplication. Instead, y'all have to multiply A ^�ane on the left, putting information technology right next to the A in the original matrix equation. And since yous have to do the same thing to both sides of an equation when y'all're solving, y'all must multiply "on the left" on the right-manus side of the equation as well, resulting in A ^�1 C . Yous cannot exist casual with your placement of the matrices; you must be precise, right, and consequent. This is the simply way to successfully cancel off A and solve the matrix equation.

---

Every bit you have seen above, changed matrices can exist very useful for solving matrix equations. Just, given a matrix, how practise yous capsize it? How do you find the inverse? The technique for inverting matrices is kind of clever. For a given matrix A and its changed A ^�1 , nosotros know we have A ^�i A = I . We're going to use the identity matrix I  in the procedure for inverting a matrix.

• Detect the inverse of the following matrix.

First, I write downwards the entries the matrix A , but I write them in a double-wide matrix:

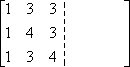
In the other half of the double-wide, I write the identity matrix:

Now I'll do matrix row operations to convert the left-mitt side of the double-wide into the identity. (As always with row operations, there is no i "right" fashion to practise this. What follows are merely the steps that happened to occur to me. Your calculations could hands look quite dissimilar.)

Now that the left-paw side of the double-wide contains the identity, the right-manus side contains the changed. That is, the changed matrix is the following:

Note that we can confirm that this matrix is the inverse of A by multiplying the ii matrices and confirming that we get the identity:   Copyright � Elizabeth Stapel 2003-2011 All Rights Reserved

Exist advised that, in "real life", the inverse is rarely a matrix filled with nice neat whole numbers similar this. With whatever luck, though, specially if you lot're doing inverses by paw, yous'll be given nice ones like this to do.

Pinnacle  | 1 | 2|  Render to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Matrix Inversion: Finding the Inverse of a Matrix." Purplemath. Bachelor from https://www.purplemath.com/modules/mtrxinvr.htm. Accessed

Source: https://www.purplemath.com/modules/mtrxinvr.htm

Posted by: vargashattacte.blogspot.com

Share this post